- GNN이란?
- GCN이란?
- GCN의 다양한 모델들 (Advanced Techniques of GCN)
- GNN이란?
- Graph neural network란?
Image, Sequential data(=Sentence) 이외에 input data구조가 graph인 경우, 이 graph data를 학습해야할 때가 있다.
(ex. 영상에서의 graph, 분자구조 graph, Social graph ...)
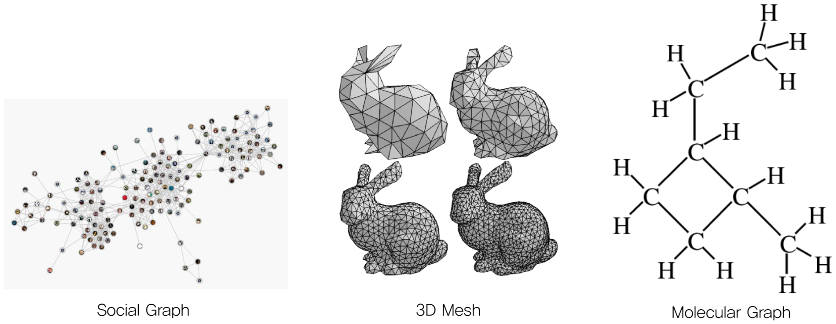
- 그렇다면 data를 어떻게 graph 형태로 나타낼 수 있을까?
Graph는 node(vertex)와 edge로 이루어져있다. 이때 node는 한 input data를 의미하고 edge는 두 data간의 relationship을 의미한다.
(ex. Social Graph에서 node는 한 명의 사람을 뜻하고 edge는 두 사람간의 relationship정보를 뜻한다.)
- 그럼 이 graph data는 어떤 식으로 표현할 것인가?
모든 node간의 relationship정보를 담고있도록 data를 표현해야하므로 이 정보들은 1) Adjacency matrix로 나타낼 수 있다. (ex. Social Graph에서 두 사람간의 relationship 정보 - 친구관계인지 아닌지)
또한 node간의 relationship정보 말고도 node(input data)자체가 가지고 있는 feature 정보가 있으므로 이는
2) Feature matrix로 나타낸다. (ex. Social Graph 에서 한 명의 사람이 갖고 있는 정보 - 이름, 나이, 국가, 학력, ... )

1) Network(Graph data) 에서 Adjacency matrix를 만드는 방법
a. 위 그림에서 가장 좌측에 있는 그림과 같은 Network가 존재할때 n개의 node를 n*n matrix로 표현해준다.
b. 이렇게 생성된 Adjacency matrix내의 value는 (Aij=i와 j의 relationship 여부)를 만족하는 value로 채워준다.
2) Feature matrix를 만드는 방법
a. 각 input data에서 이용할 feature를 먼저 select한다. (ex. RGB값 3개, transparency 1개, ... )
b. Feature matrix에서 각 row는 선정한 feature에 대해 각 node가 갖는 값을 의미한다. (ex. row1=node1의 feature값들)
- GCN이란?
- Graph Convolution Network이란?
GCN은 Graph network에 CNN에서의 Convolution 개념을 적용한 것이다.
그럼먼저 CNN에서의 특징 두 가지를 살펴보자.
1) Weight Sharing

CNN에서는 input data(ex. image)에 동일한 weight를 갖는 동일 filter를 이동하면서 연산을 진행한다.
이때 보통 stride가 filter크기보다 작게하여 이동시키므로 중복되어 연산되는 pixel이 다수 존재한다.
2) Learn local features
일반적인 MLP에서는 hidden node 들이 모든 input node와 연결지어 있어서 global feature들에 의해 학습된다.

그러나 CNN에서는 filter가 이동하면서 local feature들이랑만 연산하고 activation map을 생성하므로
각 activation map의 pixel들은 global이 아닌 local feature들에 의해서만 학습된다고 볼 수 있다.

따라서 CNN의 특징 1) Weight sharing, 2) Learn local feature를 취합해보면 CNN에서는 동일 weight의 filter를 이동하면서 local feature들에 의해 node들을 학습시킨다. 이 과정에서 많은 중복 feature(=input pixel)들이 동일 weight와 연산하기 때문에 output으로 나온 activation map의 pixel들은 근처 pixel끼리 상관 관계가 높아진다.
그렇기 때문에 Parallel Translation에 강해질 수 있다. (ex. Image를 1,2칸 shift해도 결과가 잘 나옴)
이 특성에 의해서 CNN은 근처 data끼리 상관 관계가 높은 input data에 대해 학습이 더 잘 이루어진다.
- 이 특징들을 GCN에 어떻게 똑같이 적용시킬까?
Graph의 정보를 결정하는 것은 노드에 담긴 정보이다. 따라서 local부분의 특성만 받아 동일 weight로 연산하면서 노드 정보가 update되도록 해야한다.
이제 이 과정이 어떻게 이루어지는지 자세하게 살펴보자.
1) 먼저, Graph data를 표현하기 위해 위에서 언급한대로 Adjacency matrix, A와 Feature matrix, H를 만든다.
(수식 notation을 위해 Feature matrix를 H라 칭한다.)

A행렬은 node 5개의 인접행렬이므로 5x5 shape을 갖는다.
H행렬을 보면 5x10 shape을 갖는데 row는 node개수이고 column은 선택한 feature 개수를 임의로 10개로 정한 것이다.
2) Hidden state는 W행렬과 b(bias)에 의해 update된다.
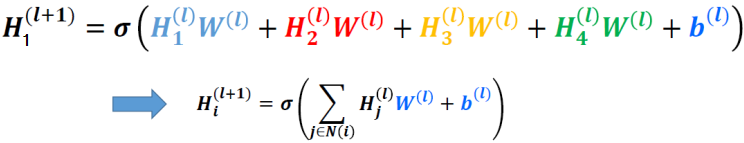
(Learn local feature)
만약 Node1이 2, 3, 4노드와 인접하고 있다고 가정하면, H1 state는 H1, H2, H3, H4에 의해서만 영향을 받아야한다.
(Weight sharing)
또한 동일 Weight 행렬을 이용하여 H1, H2, H3, H4와 연산한다.
즉, 각각의 H state는 자신과 연결된 state들과 W행렬을 곱한 후 모두 더한 값으로 update된다.
이를 일반화시키면 아래 수식으로 나타낼 수 있다.
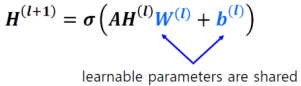
이렇게 단순히 A행렬을 곱함으로써 일반화시킬 수가 있다.
A행렬을 HW에 곱하는 이유는 다음과 같다.
각각의 H state는 자신과 연결된 state에 의해서만 영향을 받는다.
이때 H와 W행렬을 곱하여 나온 H*W행렬에서의 (i, j) value는 Hi*Wj를 뜻한다.

(W행렬의 shape은 H행렬이 5xn이라면 nxK shape을 만족해야한다. 여기서 K는 CNN에서 filter의 개수라 생각하면 된다.
위 그림에서는 임의로 W행렬을 10x5로 가정했지만 만약 filter의 개수를 64개로 하고자하면 10x64 shape이 된다.)
이때 H*W행렬에서 column N은 모든 H state들에 N번째 weight filter를 곱했을때 나온 값들이다. (weight sharing)
그러나 새롭게 update되는 H state는 자신과 relationship이 있는 state와 동일 weight filter를 곱하여 나온 값들을 모두 더한 값이여야 한다. 즉, relationship에 대한 정보는 A행렬이 담고 있으므로 A행렬과 H*W행렬을 곱하게 되면 최종 output행렬에서 (i, j) 가 나타내는 value는 A행렬에서 row i와 H*W행렬에서 column j를 곱한 값이다.
A행렬에서 row i는 node i의 relationship정보이고 H*W행렬에서 column j는 모든 H state에 j번째 weight filter를 곱한 값이다. 따라서 이 둘을 행렬 곱한것은 기존의 모든 H state에 j번째 weight filter를 곱하고 이 중에서 node i와 relationship이 있는 state만 더한 값으로 update를 한다는 뜻이다. (Learn local feature)

결과적으로 최종 ouput행렬인 H'행렬에서 row i는 node i와 relationship이 있는 노드들을 각기 다른 weight filter와 연산해서 나온 value들이다.
3) GCN을 거친 후 마지막에 Readout layer를 통해 최종적으로 classification 혹은 value를 regression한다.
CNN에서 Conv-pool layer들을 거친 후 마지막에 모든 node들 정보를 취합하기 위해 FC-layer를 거친 후 softmax를 통해 classification작업을 수행한다. 마찬가지로 Graph Neural Network에서도 graph convolution layer들을 거친 후 MLP로 모든 node 정보를 취합하고 최종적으로 regression 혹은 classification을 위해 어떤 값을 결정짓는 작업이 필요하다. 이를 GCN에서 readout-layer라고 한다.
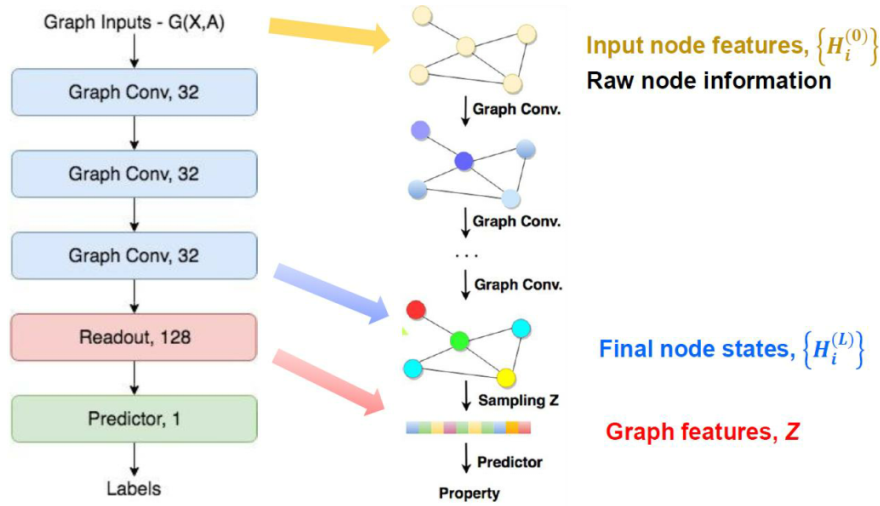
- Readout layer가 필요한 이유
같은 Network를 갖는 두 Graph가 Adjacency matrix는 서로 다를 수 있다.
모든 node간의 edge정보가 같아도 회전, 대칭에 의해 행렬내 값의 순서가 다를 수 있기 때문이다.

따라서 이런 Permutation에 대해 invariance하도록 하기위해 MLP를 곱하는 readout-layer가 필요한 것이다.
- GCN의 다양한 모델들 (Advanced Techniques of GCN)
- Inception
CNN에서 동일 Input에 대해 서로 다른 모양의 Convolution layer를 거치게 한 후 취합하는 model인 Inception 모델처럼 이를 GCN에서도 적용할 수 있다.

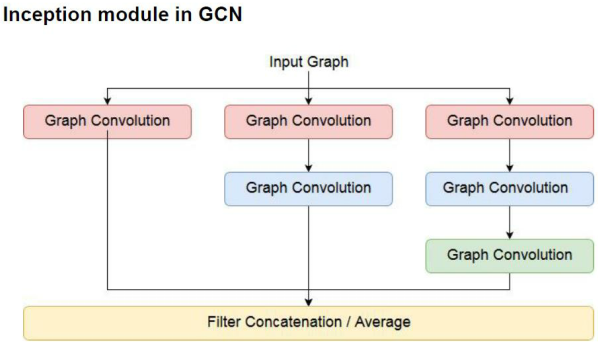
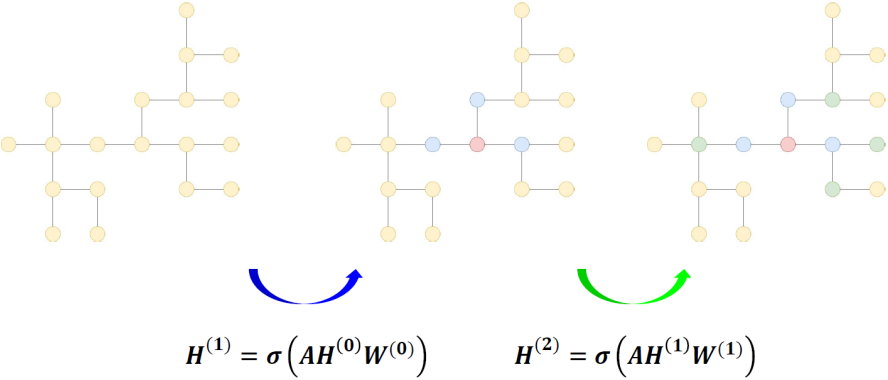
GCN에서는 graph convolution을 각기 다른 횟수만큼 거치게 한 후의 output들을 취합하는 방식으로 이루어진다.
일반적으로 graph convolution을 한 번 거친다는 것은 H state에 영향끼치는 node들이 위에서 설명했듯이 기준 노드와 relationship이 있는 인접 노드들이라는 뜻이다.
만약 graph convolution을 두 번 거치면 기준 노드로부터 거리 2만큼 떨어져있는 노드들까지 H state에 영향을 끼치게 된다.
강의출처 : https://github.com/heartcored98/Standalone-DeepLearning/blob/master/Lec9/Lec9-A.pdf
'인공지능 AI > 컴퓨터비전' 카테고리의 다른 글
| Semantic segmentation과 Instance segmentation의 차이 (0) | 2020.02.17 |
|---|---|
| translation invariance 설명 및 정리 (8) | 2020.02.16 |
| GAP(Global Average Pooling) vs FCN(Fully Convolutional Network) (4) | 2020.01.30 |
| 1-Stage detector와 2-Stage detector란? (1) | 2020.01.13 |
| 컴퓨터비전에서의 기본 용어 및 개념 정리 (2) | 2020.01.11 |



