Linear Regression vs Logistic Regression

<Regression이란?>

Supervised Learning중 하나로 input data로 discrete한 값을 예측하면 Classification

continuous한 값을 예측하면 Regression이라고 한다. 더 자세한 설명은 아래 이전글에서 확인할 수 있다.

[딥러닝] 머신러닝 기초 (1. ML Basic)

[딥러닝] 머신러닝 기초 (1. ML Basic)

 

그렇다면 Regression에서 Linear Regression(선형 회귀) 와 Logistic Regression(로지스틱 회귀)가 어떻게 다른지 보자.

---

<Linear Regression>

Linear Regression은 input data에 따른 output data의 관계를 1차원 방정식으로 구하는 것이다.

출처 : https://ko.wikipedia.org/wiki/%EC%84%A0%ED%98%95_%ED%9A%8C%EA%B7%80

따라서 Linear regression에서 값을 예측하기위해 아래의 1차 방정식을 사용한다.

 

hypothesis : 

또한 예측값을 계산하기 위해 1차 방정식을 사용하기 때문에 실제값과 예측값 사이의 loss를 계산하는데에는 최소오차제곱법을 사용하는 것이 아주 명확해보인다. 

 

Cost : 

Cost function

 

 

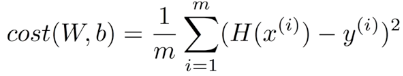
이 Cost function을 학습을 통해 최적화시키는 optimizer가 필요한데 위 Cost function은 명백하게 convex function이기 때문에 gradient descent를 사용하여 해결할 수 있다. (convex function과 GD의 관계에 대한 설명은 맨 아래에)

 

Optimizer : 

Gradient descent notation

 

 

(자세한 설명과 여러 다른 optimizer들은 아래글에서 확인할 수 있다.)

 

[딥러닝] Optimizer 종류 및 정리

[딥러닝] Optimizer 종류 및 정리

---

<Logistic Regression>

input에 대한 output과의 관계를 직선으로 알맞게 나타내지 못하는 경우가 많다. 이를 보완한게 Logistic Regression이다.

Linear Regression vs Logistic Regression

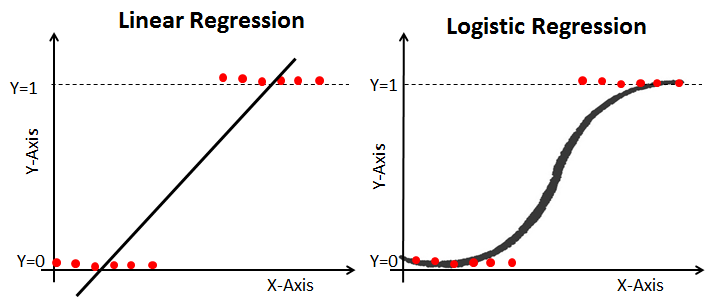
위 그림에서 알 수 있듯이 Logistic Regression은 Linear Regression에 non-linear 특성을 추가하였다.

input과 output data 관계를 곡선으로 fitting하기 위해 linear regression에서의 hypothesis에 sigmoid 활성함수를 추가하였다.

 

hypothesis : 

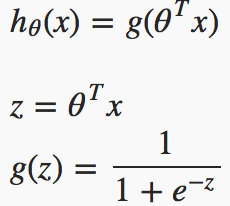
Logistic regression에서는 Linear regression에서처럼 최소오차제곱법을 cost function으로 사용하지 않는다.

Logistic regression은 sigmoid함수이므로 최소오차제곱법으로 cost function을 정의하면 위 그림에서처럼 Local minimum 부분이 여러개 생기게 된다. 따라서 이를 log를 이용하여 울퉁불퉁한 부분을 매끄럽게 펴주어야 한다.

 

Cost : 

Cost function

Logistic regression에서는 Binary Cross Entropy함수를 loss function으로 이용한다.

 

Logistic Regression에 여러 다른 activation function들이 사용될 수 있는데 보통 일반적으로 이처럼 sigmoid를 사용하여 hypothesis값을 0~1사이 값으로 만들어서 binary classification을 하는데 많이 이용된다.

따라서 binary classification이라 가정했을때 위 cost function은 두 가지 경우로 생각해볼 수 있다.

1. y=0인 경우) 예측값이 0일수록 cost가 0에 수렴한다.

2. y=1인 경우) 예측값이 1일수록 cost가 0에 수렴한다.

 

 

---

*Convex function과 Gradient descent

 

Linear Regression은 cost function이 아래 그림처럼 convex function이기 때문에 GD를 사용하면 global minimum을 계산할 수 있다.

Convex function

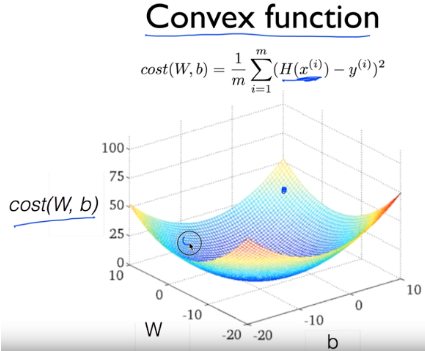
따라서 Cost function이 convex인지 확인만 되면 GD를 사용하여 손쉽게 최적화 시킬 수 있다.

그러나 convex하지 않은데 GD를 이용하면 초기값에 따라서 다른 해가 구해지므로 주의해야한다.