<개요>
신경망모델의 각 layer에서는 input 값과 W, b를 곱, 합연산을 통해 a=WX+b를 계산하고 마지막에 활성화 함수를 거쳐 h(a)를 출력한다. 이렇게 각 layer마다 sigmoid, softmax, relu 등.. 여러 활성화 함수를 이용하는데 그 이유가 뭘까?
<XOR문제> - 선형분류기의 한계
인공신경망에 대한 연구가 한계를 맞게된 첫 과제는 바로 XOR문제였다.
아래 그림에서 확인할 수 있듯이 기존의 퍼셉트론은 AND와 OR문제는 해결할 수 있었지만 선형 분류기라는 한계에 의해 XOR과 같은 non-linear한 문제는 해결할 수 없었다.

그리고 이를 해결하기 위해 나온 개념이 hidden layer이다. 그러나 이 hidden layer도 무작정 쌓기만 한다고 해서 퍼셉트론을 선형분류기에서 비선형분류기로 바꿀 수 있는 것은 아니다.
왜냐하면 선형 시스템이 아무리 깊어지더라도 f(ax+by)=af(x) + bf(y)의 성질 때문에 결국 하나의 layer로 깊은 layer를 구현할 수 있기 때문이다.
즉, linear한 연산을 갖는 layer를 수십개 쌓아도 결국 이는 하나의 linear 연산으로 나타낼 수 있다.
<활성화 함수>
이에 대한 해결책이 바로 활성화 함수(activation function)이다.
활성화 함수를 사용하면 입력값에 대한 출력값이 linear하게 나오지 않으므로 선형분류기를 비선형 시스템으로 만들 수 있다.
* 따라서 MLP(Multiple layer perceptron)는 단지 linear layer를 여러개 쌓는 개념이 아닌 활성화 함수를 이용한 non-linear 시스템을 여러 layer로 쌓는 개념이다.
활성화함수를 사용하면 왜 입력값에 대한 출력값을 비선형으로 만들 수 있는지는 함수의 생김새만 봐도 명확하다.
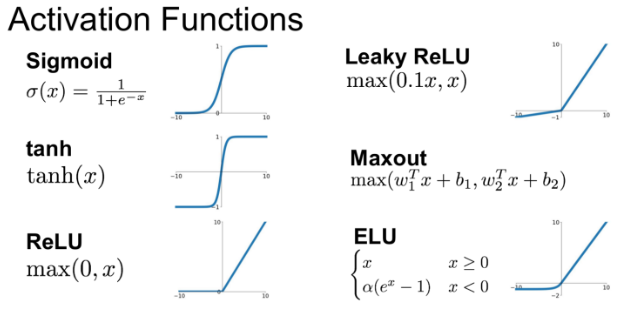
(다양한 활성화 함수에 대한 설명은 아래 글을 참조)
[딥러닝] 활성화 함수(activation function)종류 및 정리
[딥러닝] 활성화 함수(activation function)종류 및 정리
<활성화 함수 종류> <시그모이드(Sigmoid)> 수식 : output값을 0에서 1사이로 만들어준다. 데이터의 평균은 0.5를 갖게된다. 위 그림에서 시그모이드 함수의 기울기를 보면 알 수 있듯이 input값이 어느정도 크..
ganghee-lee.tistory.com
위의 XOR을 sigmoid활성화 함수를 이용하여 해결해보면 아래 그림과 같다.

<요약>
결론적으로 활성화 함수는 입력값을 non-linear한 방식으로 출력값을 도출하기 위해 사용한다.
이를 통해 linear system을 non-linear한 system으로 바꿀 수 있게 되는 것이다.
그러나, 이렇게 활성화 함수를 이용하여 비선형 시스템인 MLP를 이용하여 XOR는 해결될 수 있지만, MLP의 파라미터 개수가 점점 많아지면서 각각의 weight와 bias를 학습시키는 것이 매우 어려워 다시 한 번 침체기를 겪게되었다.
그리고 이를 해결한 알고리즘이 바로 역전파(Back Propagation)이다.
[딥러닝] 역전파 backpropagation이란?
<개요> 이전 글에서 설명했듯이 활성화 함수를 적용시킨 MLP에서 XOR과 같은 non-linear 문제들은 해결할 수 있었지만 layer가 깊어질수록 파라미터의 개수가 급등하게 되고 이 파라미터들을 적절하게 학습시키는..
ganghee-lee.tistory.com
'인공지능 AI > 딥러닝' 카테고리의 다른 글
| 활성화 함수(activation function)종류 및 정리 (1) | 2020.01.10 |
|---|---|
| 딥러닝 역전파 backpropagation이란? (0) | 2020.01.09 |
| Linear Regression vs Logistic Regression (0) | 2020.01.09 |
| Objective Function, Loss Function, Cost Function의 차이 (0) | 2020.01.09 |
| 딥러닝 기본 용어 및 개념정리 (0) | 2020.01.04 |



