<개요>
이전 글에서 설명했듯이 활성화 함수를 적용시킨 MLP에서 XOR과 같은 non-linear 문제들은 해결할 수 있었지만 layer가 깊어질수록 파라미터의 개수가 급등하게 되고 이 파라미터들을 적절하게 학습시키는 것이 매우 어려웠다.
그리고 이는 역전파 알고리즘이 등장하게 되면서 해결되었고 결론적으로 여러 layer를 쌓은 신경망 모델을 학습시키는 것이 가능해졌다.
<역전파>
역전파 알고리즘은 출력값에 대한 입력값의 기울기(미분값)을 출력층 layer에서부터 계산하여 거꾸로 전파시키는 것이다.
이렇게 거꾸로 전파시켜서 최종적으로 출력층에서의 output값에 대한 입력층에서의 input data의 기울기 값을 구할 수 있다.
이 과정에는 중요한 개념인 chain rule이 이용된다.
출력층 바로 전 layer에서부터 기울기(미분값)을 계산하고 이를 점점 거꾸로 전파시키면서 전 layer들에서의 기울기와 서로 곱하는 형식으로 나아가면 최종적으로 출력층의 output에 대한 입력층에서의 input의 기울기(미분값)을 구할 수가 있다. 이를 그림으로 나타내면 아래와 같다.
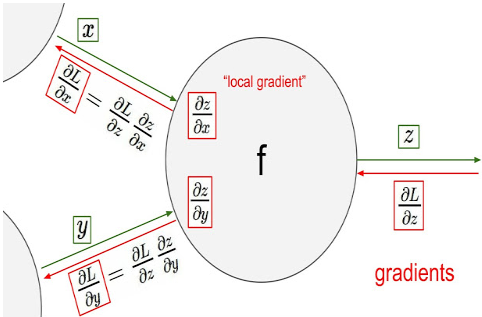
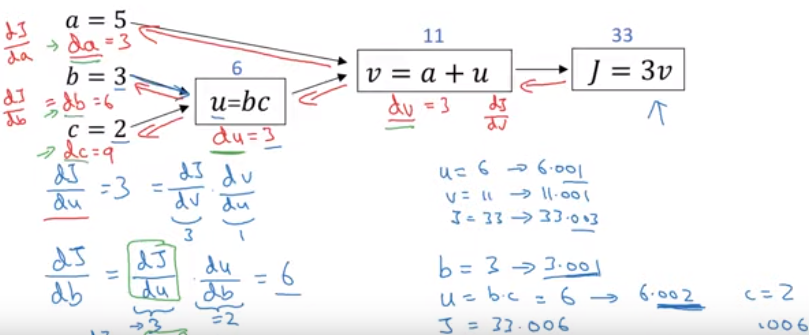
1. 그럼 이렇게 기울기(미분값)을 구하는 이유는 무엇이고
2. 최종 output에 대한 기울기 값을 각 layer별로 구하는 이유가 무엇일까??
<Gradient Descent>
역전파 알고리즘이 해결한 문제가 바로 파라미터가 매우 많고 layer가 여러개 있을때 가중치w와 b를 학습시키기 어려웠다는 문제이다. 그리고 이는 역전파 알고리즘으로 각 layer에서 기울기 값을 구하고 그 기울기 값을 이용하여 Gradient descent 방법으로 가중치w와 b를 update시키면서 해결된 것이다.
즉, layer에서 기울기 값을 구하는 이유는 Gradient descent를 이용하여 가중치를 update하기 위함이다.
이때 각 layer의 node(parameter)별로 학습을 해야하기 때문에 각 layer의 node별로 기울기 값을 계산해야하는 것이다.
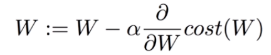
'인공지능 AI > 딥러닝' 카테고리의 다른 글
| Train / Test / Validation set의 차이 (10) | 2020.01.15 |
|---|---|
| 활성화 함수(activation function)종류 및 정리 (1) | 2020.01.10 |
| 활성화 함수(activation function)을 사용하는 이유 (0) | 2020.01.09 |
| Linear Regression vs Logistic Regression (0) | 2020.01.09 |
| Objective Function, Loss Function, Cost Function의 차이 (0) | 2020.01.09 |



