<활성화 함수 종류>

<시그모이드(Sigmoid)>

수식 :

output값을 0에서 1사이로 만들어준다. 데이터의 평균은 0.5를 갖게된다.
위 그림에서 시그모이드 함수의 기울기를 보면 알 수 있듯이 input값이 어느정도 크거나 작으면 기울기가 아주 작아진다. 이로인해 생기는 문제점은 vanishing gradient현상이 있다.
Vanishing gradient
이렇게 시그모이드로 여러 layer를 쌓았다고 가정하자. 그러면 출력층에서 멀어질수록 기울기가 거의 0인 몇몇 노드에 의해서 점점 역전파해갈수록, 즉 입력층 쪽으로갈수록 대부분의 노드에서 기울기가 0이되어 결국 gradient가 거의 완전히 사라지고만다. 결국 입력층쪽 노드들은 기울기가 사라지므로 학습이 되지 않게 된다.
시그모이드를 사용하는 경우
대부분의 경우에서 시그모이드함수는 좋지 않기때문에 사용하지 않는다. 그러나 유일한 예외가 있는데
binary classification경우 출력층 노드가 1개이므로 이 노드에서 0~1사이의 값을 가져야 마지막에 cast를 통해(ex. 0.5이상이면 1, 미만이면 0) 1혹은 0값을 output으로 받을 수 있다. 따라서 이때는 시그모이드를 사용한다.
요약
장점) binary classification의 출력층 노드에서 0~1사이의 값을 만들고 싶을때 사용한다.
단점) Vanishing gradient - input값이 너무 크거나 작아지면 기울기가 거의 0이된다.
<Tanh>

수식 :
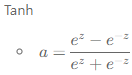
그림에서 보면 알 수 있듯이 시그모이드 함수와 거의 유사하다. 차이는 -1~1값을 가지고 데이터의 평균이 0이라는 점이다. 데이터의 평균이 0.5가 아닌 0이라는 유일한 차이밖에 없지만 대부분의 경우에서 시그모이드보다 Tanh가 성능이 더 좋다. 그러나 시그모이드와 마찬가지로 Vanishing gradient라는 단점이 있다.
결론
장점) output데이터의 평균이 0으로써 시그모이드보다 대부분의 경우에서 학습이 더 잘 된다.
단점) 시그모이드와 마찬가지로 Vanishing gradient현상이 일어난다.
<ReLU>

수식 :
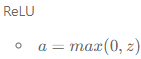
대부분의 경우 일반적으로 ReLU의 성능이 가장 좋기때문에 ReLU를 사용한다.
"Hidden layer에서 어떤 활성화 함수를 사용할지 모르겠으면 ReLU를 사용하면 된다" - Andrew ng
대부분의 input값에 대해 기울기가 0이 아니기 때문에 학습이 빨리 된다. 학습을 느리게하는 원인이 gradient가 0이 되는 것인데 이를 대부분의 경우에서 막아주기 때문에 시그모이드, Tanh같은 함수보다 학습이 빠르다.
그림을 보면 input이 0보다 작을 경우 기울기가 0이기 때문에 대부분의 경우에서 기울기가 0이 되는것을 막아주는게 납득이 안 될수 있지만 실제로 hidden layer에서 대부분 노드의 z값은 0보다 크기 때문에 기울기가 0이 되는 경우가 많지 않다.
단점으로는 위에서 언급했듯이 z가 음수일때 기울기가 0이라는 것이지만 실제로는 거의 무시할 수 있는 수준으로 학습이 잘 되기 때문에 단점이라 할 수도 없다.
결론
장점) 대부분의 경우에서 기울기가 0이 되는 것을 막아주기 때문에 학습이 아주 빠르게 잘 되다.
hidden layer에서 활성화 함수 뭐 써야할지 모르겠으면 그냥 ReLU를 쓰면 된다.
<leaky ReLU>
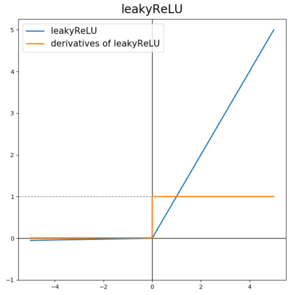
수식 :
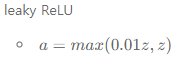
ReLU와 유일한 차이점으로는 max(0, z)가 아닌 max(0.01z, z)라는 점이다.
즉, input값인 z가 음수일 경우 기울기가 0이 아닌 0.01값을 갖게 된다.
leaky ReLU를 일반적으로 많이 쓰진 않지만 ReLU보다 학습이 더 잘 되긴 한다.
결론
장점) z가 음수일때 기울기가 0이 아닌 0.01을 갖게 하므로 ReLU보다 학습이 더 잘 된다.
[딥러닝] 활성화 함수(activation function)을 사용하는 이유
[딥러닝] 활성화 함수(activation function)을 사용하는 이유
<개요> 신경망모델의 각 layer에서는 input 값과 W, b를 곱, 합연산을 통해 a=WX+b를 계산하고 마지막에 활성화 함수를 거쳐 h(a)를 출력한다. 이렇게 각 layer마다 sigmoid, softmax, relu 등.. 여러 활성화 함수..
ganghee-lee.tistory.com
'인공지능 AI > 딥러닝' 카테고리의 다른 글
| Train / Test / Validation set의 차이 (10) | 2020.01.15 |
|---|---|
| 딥러닝 역전파 backpropagation이란? (0) | 2020.01.09 |
| 활성화 함수(activation function)을 사용하는 이유 (0) | 2020.01.09 |
| Linear Regression vs Logistic Regression (0) | 2020.01.09 |
| Objective Function, Loss Function, Cost Function의 차이 (0) | 2020.01.09 |



